Եռանկյան երկու կողմերի միջնակետերը միացնող հատվածը կոչվում է այդ եռանկյան միջին գիծ:

Միջին գծի հատկությունը

Եռանկյան միջին գիծը զուգահեռ է եռանկյան կողմերից մեկին և հավասար է այդ կողմի կեսին:

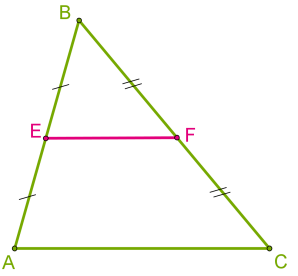
DF∥BC DF=BC/2

Յուրաքանչյուր եռանկյուն ունի երեք միջին գիծ:

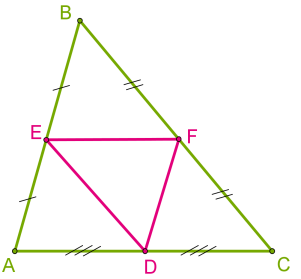
Միջին գծերն են DE, EF և DF հատվածները:

Թալեսի* թեորեմը

Եթե անկյան կողմերը հատող զուգահեռ ուղիղները անկյան մի կողմի վրա անջատում են հավասար հատվածներ, ապա նրանք անկյան մյուս կողմի վրա ևս անջատում են հավասար հատվածներ:

Թալեսի թեորեմը օգտագործում են տրված հատվածը մի քանի հավասար մասերի բաժանելու համար:

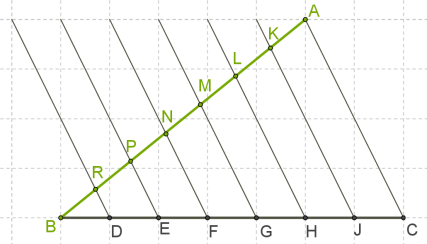
Պետք է AB հատվածը բաժանել 7 հավասար մասերի:  

Գծենք անկյուն, որի մի կողմի վրա ընկած է AB հատվածը: BC կողմը գծենք վանդակների միջոցով՝ հորիզոնական ուղղությամբ: Վանդակները օգտագործում ենք կողմը 7 հավասար մասերի բաժանելու համար՝ BD=DE=EF=FG=GH=HJ=JC:

Երկու հատվածների ծայրակետերը միացնում ենք և ստանում AC հատվածը: J,H,G,F,E,D կետերից տանենք AC -ին զուգահեռ 7 ուղիղներ (նորից օգտագործում ենք վանդակները):

Եթե BD=DE=EF=FG=GH=HJ=JC և AC∥JK∥HL∥GM∥FN∥EP∥DR, ապա, ըստ Թալեսի թեորեմի՝ BR=RP=PN=NM=ML=LK=KA:

*Թեորեմը կոչվում է հին հույն գիտնական Թալես Միլեթացու (մ.թ.ա. մոտ 625-547 թթ.) անունով:

Առաջադրանքներ։

1․ Գրել եռանկյան միջին գծի սահմանումը։

Եռանկյան երկու կողմերի միջնակետերը միացնող հատվածը կոչվում է այդ եռանկյան միջին գիծ:

2․ Գրել միջին գծի հատկությունը։

Եռանկյան երկու կողմերի միջնակետերը միացնող հատվածը կոչվում է այդ եռանկյան միջին գիծ:

3․ RS -ը  ABC եռանկյան միջին գիծն է՝ R∈AB, S∈AC։ Ընտրել  ճիշտ տարբերակը:

ա) RS∥BC

բ) RS⊥AB

գ) երկուսն էլ ճիշտ են

4․ LMN եռանկյան մեջ GH-ը միջին գիծ է՝  G∈LM, H∈LN: Միջին գծի  վերաբերյալ, ո՞ր պնդումն է ճիշտ: Ընտրել  ճիշտ պատասխանը:

ա) GH=2MN

բ) GH=MN/2

գ) երկուսն էլ ճիշտ են