Մեզ արդեն հայտնի է կոորդինատների ուղղանկյուն համակարգի հասկացությունը: Կոորդինատային ուղղանկյուն համակարգ ներմուծելու համար պետք է կատարել հետևյալը.

1. Տանել երկու փոխուղղահայաց ուղիղներ, որոնց վրա նշված են թվերի աճման ուղղությունները (սլաքի միջոցով):

Հորիզոնական ուղիղը կոչվում է աբսցիսների առանցք: Ուղղահայաց ուղիղը՝ օրդինատների:  

2. Ուղիղների հատման կետը կոչվում է կոորդինատային համակարգի սկզբնակետ: Սովորաբար այն նշանակում են O տառով:

3. Յուրաքանչյուր ուղղի վրա նշված է միավոր երկարությամբ հատված (մասշտաբ): 

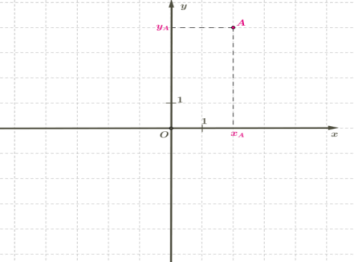
Հարթության յուրաքանչյուր կետ ունի երկու կոորդինատ՝ x և y (աբսցիսը և օրդինատը): A(xA;yA) կետի աբսցիսը և օրդինատը գտնելու համար այդ կետից իջեցնում ենք ուղղահայացներ՝ համապատասխանաբար աբսցիսների և օրդինատների առանցքների վրա:

Վերևի նկարի վրա ցուցադրված է A(2;4) կետը: A կետի աբսցիսը հավասար է 2-ի, իսկ օրդինատը՝ 4-ի:

Կոորդինատային յուրաքանչյուր առանցք հարթությունը տրոհում է երկու կիսահարթությունների, իսկ երկուսը միասին հարթությունը տրոհում են 4 քառորդի:

Կոորդինատային համակարգ կառուցելիս կարևոր է հիշել երկու հանգամանք:

1) Երկու կոորդինատային առանցքների վրա պետք է ընտրել նույն մասշտաբի միավորը:

2) Աբսցիսների առանցքի վրայով դեպի աջ շարժվելիս մեծանում է աբսցիսը, իսկ օրդինատների առանցքի վրայով դեպի վերև շարժվելիս՝ օրդինատը:

Հատվածի միջնակետի կոորդինատները

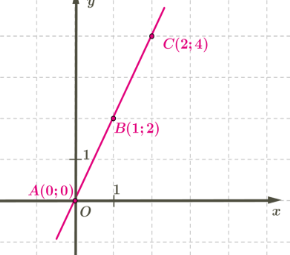
Դիտարկենք վերևի նկարի O(0;0) և C(2;4) կետերը միացնող OC հատվածը:

Նկարից երևում է, որ OC հատվածը 2 և 4 կողմերով ուղղանկյան անկյունագիծն է, և նրա միջնակետը B(1;2) կետն է. ուղղանկյան անկյունագծերը հատվելիս կիսվում են:

Նկատում ենք, որ B(1;2) կետի կոորդինատները O(0;0) և C(2;4) կետերի կոորդինատների միջոցով արտահայտվում են հետևյալ կերպ՝

1=(0+2)/2, 2=(0+4)/2

Այս օրինաչափությունը տեղի ունի նաև ընդհանուր դեպքում:

Եթե կոորդինատային հարթության վրա վերցված են երկու կետեր՝ K(x0;y0)  և  L(x1;y1), ապա KL հատվածի  M(x;y) միջնակետի կոորդինատները հավասար են՝

x=(x₀+x₁)/2, y=(y₀+y₁)/2

Այսպիսով, հարթության վրա տրված երկու կետերը միացնող հատվածի միջնակետի կոորդինատները հավասար են ծայրակետերի համապատասխան կոորդինատների միջին թվաբանականներին՝

x=(x₀+x₁)/2, y=(y₀+y₁)/2

Առաջադրանքներ։

1․ Ո՞ ր քառորդում են գտնվում  հետևյալ կետերը՝ A(13;−40),  B(−40;15),  C(18;10)   D(−40;−26), M(−11;−47), K(−14;13):

A(13;−40) – IV քառորդ

B(−40;15) – II քառորդ

C(18;10) – I քառորդ

D(−40;−26) – III քառորդ

M(−11;−47) – III քառորդ

K(−14;13) – II քառորդ

2․ Գտնել  օրդինատների առանցքի նկատմամբ (25;7) կոորդինատներով կետին համաչափ կետը:

x առանցքի նկատմամբ համաչափ կետը – ( 25 ; − 7 )

y առանցքի նկատմամբ համաչափ կետը – ( − 25 ; 7 )

Մանկան գագաթների կամ արմատային համաչափությունը – ( − 25 ; − 7 )

3․ Կոորդինատային հարթության վրա վերցված է (0;34) կոորդինատներով կետը: Որոշել x-երի առանցքի նկատմամբ նրան համաչափ կետի կոորդինատները:

( 0 ; – 34 )

4․ Գրել P(23;2) կետի հեռավորությունը աբսցիսների առանցքից:

Պատ․՝ 2 միավոր