Այսօր չորեքշաբթի է՝ ճամբարային երրորդ օրը։ Այսօր մենք տարազի էսքիզները նկարեցինք կտորի վրա։ Իսկ հետո Ավագ դպրոցի սովորողների հետ քննարկեցինք <<Արհեստական բանականության>> մասին։

ֆիզիկա

Պատմության բաժնում հոկտեմբեր ամսից ունեմ 3 նյութ։ Շատ հետաքրքիր դասեր ենք ունեցել։

Համաշխարհային պատմություն 7, Պատմություն 7, Արատտա

1) OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք <AOB-ն, եթե <AOE=56⁰, <EOB=123⁰34’։

երկրաչափություն

Урок 1

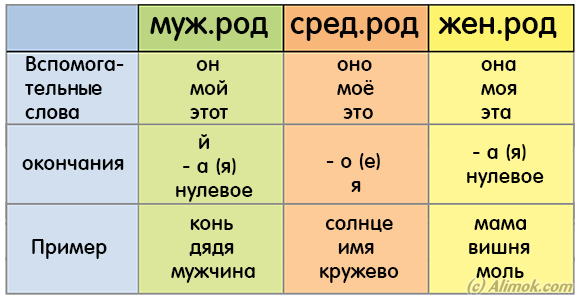
Вы уже хорошо знаете, что в русском языке существительные могут быть мужского (он), женского (она) или среднего (оно) рода.

Русский язык

երկրաչափություն

Պատասխանել հարցերին․

կենսաբանություն

1- My family often (go) goes out for dinner.

English

Տառեր պարունակող ոչ զրոյական միանդամը եթե ունի միայն մեկ թվային արտադրիչ, որը գրված է առաջին տեղում, իսկ յուրաքանչյուր տառ հանդես է գալիս միայն մեկ անգամ՝գրված որոշակի աստիճանի տեսքով, ընդ որում՝ տառերը գրված են այբբենական կարգով, ասում են, որ այդպիսի միանդամն ունի կատարյալ տեսք:

Օրինակ՝  3a²b  կատարյալ տեսքի է

                  aab3  կատարյալ տեսքի չէ

Տառեր պարունակող ոչ զրոյական կատարյալ տեսքով գրված միանդամի թվային արտադրիչը անվանում են միանդամի գործակից:

Օրինակ՝ -12ab⁴c կատարյալ տեսքով գրված միանդամի գործակիցը՝ -12-ն է:

Եթե ոչ զրոյական միանդամը ունի միայն տառային արտադրիչներ, ապա համարում են, որ նրա գործակիցը 1 է: 

Օրինակ՝  x⁵yz⁷  միանդամի գործակիցը 1 է:

Ցանկացած իրական թիվ համարվում է կատայալ տեսքով գրված միանդամ:

Օրինակ՝ -3; 123; -⅘   կատրայալ տեսքի միանդամներ են:

Զրոյական միանդամի կատարյալ տեսքը 0-ն է:

Ցանկացած միանդամ կարելի է բերել կատարյալ տեսքի:

Օրինակ՝ a(-3)a³b²(-4)b=12a⁴b³

                 x²y0z=0

Կատարյալ տեսքի ոչ զրոյական միանդամի աստիճան կոչվում է նրա մեջ մտնող բոլոր տառերի աստիճանների գումարը:

Օրինակ՝ 4x⁵y -ը  6 աստիճանի միանդամ է:

0-ից տարբեր թիվ հանդիսացող միանդամի աստիճանը 0 է, իսկ 0 թիվը միակ միանդամն է, որի աստիճանը չի սահմանվում:

Սահամնում։ Կատայալ տեսքի ոչ զրոյական  միանդամներն անվանում են նման, եթե նրանք իրար հավասար են, կամ տարբերվում են միայն իրենց գործակիցներով:

Օրինակ՝ 3ab և 5ab նման են, որովհետև տարբերվում են միայն գործակցով:

Պարզելու համար՝ նմա՞ն են արդյոք տրված միանդամները, նրանց սկզբում պետք է բերել կատարյալ տեսքի: 

Նման միանդամների գումարը հավասար է մի միանդամի, որը նման է դրանցից յուրաքանչյուրին և գործակիցը հավասար է այդ միանդամների գործակիցների գումարին: Նույն ձևով էլ հանումը:

Օրինակ՝ 3a³b+4a³b=(3+4)a³b

                 2xy-4xy=(2-4)xy=-2xy

Այս գործողությունները կոչվում են նման անդամների միացում:

Առաջադրանքներ

1) Ո՞ր միանդամներն անվանում նման:

Եթե նրանք իրար հավասար են, կամ տարբերվում են միայն իրենց գործակիցներով նրանց անվանում են մնան միանդամներ:

    Ինչպե՞ս ենք գումարում, հանում նման միանդամները:

Գումարել և հանել կարելի է միայն նման միանդամները:Ոչ զրոյական միանդամներն անվանում են նման, եթե կատարյալ տեսքի բերելուց հետո դրանք իրար հավասար են կամ տարբերվում են միայն իրենց գործակիցներով: 

2) Տրված միանդամների մեջ գտեք նմանները

ա) 2a³b;  3a⁴b²; 4a³b;  80a⁴b²; a³b;  -a⁴b²;  a;  -c;  6px; 6a⁴b²; -5px

բ)  0a²b³; -3a³b²; 0ab; 12a²b³; 2a³b²

3) Գտեք նման միանդամների գումարին հավասար միանդամը

ա) 3m+5m

բ)  15a²b+14a²b+7a²b

գ)  25b²c³+(-27)b²c³+7b²c³

4) Գտեք նման միանդամների տարբերությանը հավասար միանդամը

ա) a-3a=-2a

բ) 10b-18b

գ) 3bc-17bc

դ) mk-3mk

ե) 4b²c-12b²c

զ) 18a³b⁵-9a³b⁵

5) Կատարեք նման անդամների միացում

ա) 6a⁸b²+7a⁸b²+(-2)a⁸b²

բ) 0c²e⁵+4c²e⁵-16c²e⁵